Implicit orientation of a holomorphic manifold
When I first started learning analytic geometry (the complex analogue to algebraic geometry), I recall asking my advisor why the local intersection number is defined with no regards for orientation. At the time, he simply said that complex manifolds are assumed to be positively oriented, which I didn't pay much attention to since I was too busy trying to wrap my head around more elementary concepts, such as the Zariski topology of the spectre of a Noetherian ring.
Fast forward to a few days ago. A friend was telling us about Chern classes, and he mentioned once again orientation and holomorphic manifolds. However, he was more specific on the question:
...and we can assume that [a complex manifold] always has a well-defined orientation since “the complex numbers have an implicit orientation”, or something like that [sic].
I recently happened to have attended a mini-course about Floer homology, which involves endowing real manifolds of even dimension with a complex structure on the tangent spaces, so I realised that you could use the latter to explain the former. For our intents and purposes, a complex structure is a $2\times 2$ matrix $J$ such that $J^2$ is the identity matrix with a minus sign.
Any complex number $x+iy$ can be represented in the real plane in two ways: as a vector $(x,y)$ and as a matrix
$$J(x+iy)=\begin{pmatrix}x&-y \\ y&x\end{pmatrix}.$$
In particular, $J(i)$ is a complex structure (as per our definition)! Not only that, but we also have $J(a+ib)=a J(1)+ b J(i)$, so complex multiplication can be recovered using this $J$ matrix. Note that $J$ (seen as a mapping $\mathbb{R}^2 \to \mathbb{R}^2$) describes an counter-clockwise rotation, which corresponds to the positive orientation on the plane.
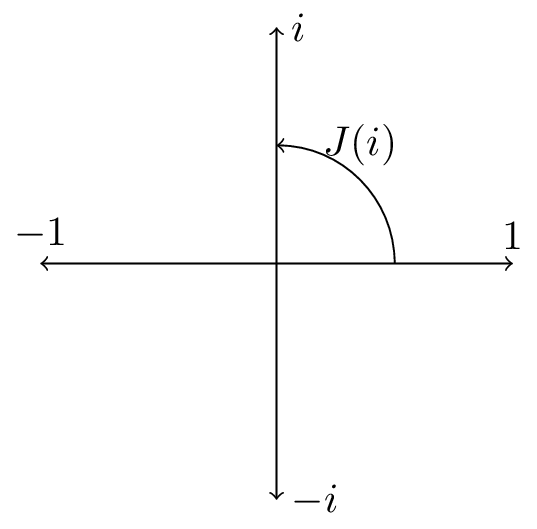
The transpose of $a+ib$ can be described in terms of the $J$ matrix as $aJ(1)+bJ(-i)$. However, $J(-i)$ corresponds to a clockwise rotation, which is the negative orientation on the plane.
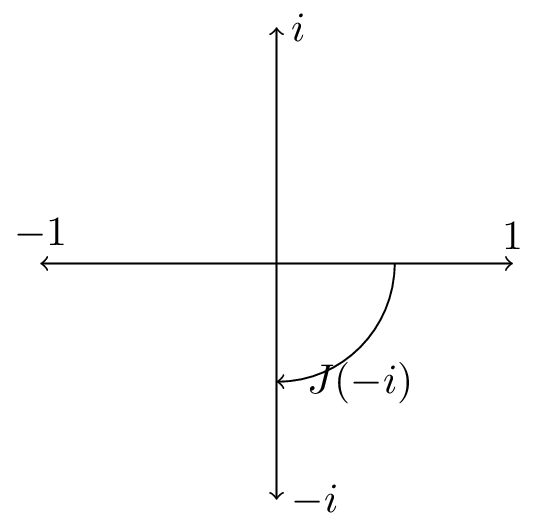
Since the mapping $z \mapsto \overline z$ is not holomorphic, this means that only one of the two orientations on the plane is compatible with the complex derivative!